Библиотека конечных элементов для линейных задач

№№ КЭ

Наименование КЭ

Признак схемы

Плоскость расположения

Степени свободы

Комментарий

1

2

3

4

5

6

10

Универсальный стержень

1

2

3

4

5

произ-вольно

X, Y, Z, UX, UY, UZ

1.Допускается наличие упругого основания в двух плоскостях.

2.Предусмотрен учет сдвиговой жесткости и обжатия.

1

Стержень плоской фермы

1

XOZ

X, Z

Частный случай

КЭ-10

2

Стержень плоской рамы

2

XOZ

X, Z, UY

Частный случай

КЭ-10

3

Стержень балочного ростверка

3

XOY

Z, UX, UY

Частный случай

КЭ-10

4

Стержень пространственной фермы

4

произ-вольно

X, Y, Z

Частный случай

КЭ-10

5

Пространственный стержень без учета сдвига

5

произ-вольно

X, Y, Z, UX,

UY, UZ

Частный случай

КЭ-10

11

Универсальный прямоугольный конечный элемент плиты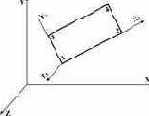

3,5

XOY

Z, UX, UY

Допускается наличие упругого основания.

1

2

3

4

5

6

12

Универсальный треугольный конечный элемент плиты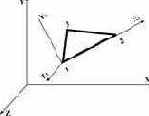

3,5

XOY

Z, UX, UY

Допускается наличие упругого основания.

21 (23)

Универсальный прямоугольный конечный элемент плоской задачи теории упругости (балка-стенка)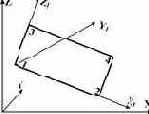

1,2,5 (4,5)

XOZ произ-вольно

X, Z

(X, Y, Z)

Допускаются следующие виды плоской задачи теории упругости: плоское напряженное состояние; плоская деформация.

22 (24)

Универсальный треугольный конечный элемент плоской задачи теории упругости (балка-стенка)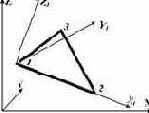

1,2,5 (4,5)

XOZ

произ-вольно

X, Z

(X, Y, Z)

1

2

3

4

5

6

27

(30)

Универсальный четырехугольный (восьмиузловой) конечный элемент плоской задачи теории упругости (балка-стенка)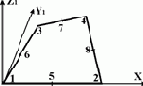

4, 5

(1, 2)

произ-вольно

(XOZ)

X, Y, Z

(X, Z)

Наличие

узлов 5, 6, 7 и

8 необязательно.

31

Параллелепипед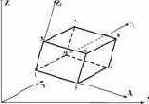

4, 5

произ-вольно

X, Y, Z

32

Тетраэдр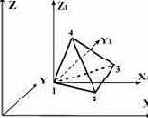

4, 5

произ-вольно

X, Y, Z

33

Трехгранная призма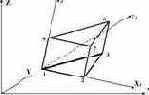

4, 5

произ-вольно

X, Y, Z

1

2

3

4

5

6

34

Универсальный пространственный

изопараметрический шестиузловой

конечный элемент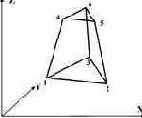

4, 5

произ-вольно

Z, UX, U, Y

36

Универсальный пространственный изопараметрический восьмиузловой конечный элемент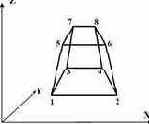

4, 5

произ-вольно

X ,Y, Z

41

Универсальный прямоугольный элемент оболочки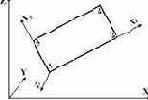

5

произ-вольно

X, Y, Z UX, UY, UZ

Допускается наличие упругого основания.

42

Универсальный треугольный элемент оболочки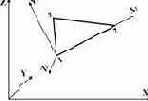

5

произ-вольно

X, Y, Z, UX, UY, UZ

1

2

3

4

5

6

44

Универсальный четырехугольный конечный элемент оболочки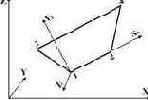

5

произ-вольно

X, Y, Z, UX, UY, UZ

51

Одноузловой элемент связи конечной жесткости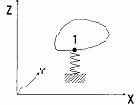

5

вдоль осей глобальной системы координат

X, Y, Z, UX, UY, UZ

Применяется для учета податливости опорной связи

53

Законтурный двухузловой конечный элемент упругого основания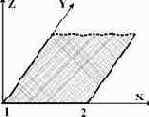

3,4,5

XOY

Z

Учитывает влияние полосы грунта за пределами конструкции

54

Законтурный одноузловой конечный элемент упругого основания

3 4 5

XOY

Z

Учитывает сдвиговое влияние угловой зоны грунта за пределами конструкции

1

2

3

4

5

6

55

Упругая связь между узлами

1-5

вдоль осей глобальной системы координат

X, Y, Z, UX, UY, UZ

Учет податливости стыков в конструкции