Библиотека конечных элементов для геометрически нелинейных задач
Моделирование геометрической нелинейности производится с помощью конечных элементов, учитывающих изменение геометрии конструкции и работу мембранной группы напряжений (усилий) на новых перемещениях, что позволяет рассчитывать мембранные и вантовые конструкции.
При расчете геометрически нелинейных систем считается, что закон Гука соблюдается. На каждом шаге происходит учет мембранной группы усилий (для стержней – учет продольной силы) при построении матрицы жесткости.
Для решения геометрически нелинейных задач реализован автоматический выбор шага нагружения. Это сделано для того, чтобы при расчете изначально геометрически изменяемых систем, прежде всего найти их равновесную форму (например, нить, изначально имеющая форму параболы, нагружена сосредоточенной силой). При этом для достижения необходимой точности первый шаг должен быть достаточно мелким.
Состав библиотеки приведен в табл. 7.8.
Таблица 7.8
|
№№ КЭ |
Наименование КЭ |
Признак схемы |
Плоскость расположения |
Степени свободы |
|
1 |
2 |
3 |
4 |
5 |
|
310 |
Универсальный пространственный стержневой конечный элемент (нить) 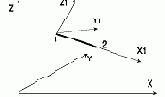 |
1 2 4 5 |
произ-вольно |
U,V,W UX, UY, UZ |
|
308 |
Специальный стержневой конечный элемент предварительного натяжения  |
1 2 4 5 |
произ-вольно |
U,V,W |
|
1 |
2 |
3 |
4 |
5 |
|
341 |
Прямоугольный элемент оболочки (мембрана) 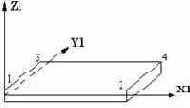 |
5 |
произ-вольно |
U, V, W, UX, UY, UZ |
|
342 |
Треугольный элемент оболочки (мембрана) 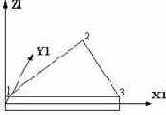 |
5 |
произ-вольно |
U,V,W, UX, UY, UZ |
|
344 |
Четырехугольный элемент оболочки (мембрана) 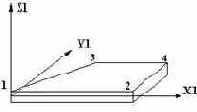 |
5 |
произ-вольно |
U,V,W, UX, UY, UZ |
