КЭ объемного НДС
Определение главных напряжений в этом случае производится из решения кубического уравнения.

где :

Корни уравнения (12.7):

где :

Главные напряжения:

Затем вычисляются направляющие косинусы углов наклона осей к осям местной системы координат КЭ из системы уравнений вида:

где i=1,2,3.
Решив систему трижды, получим матрицу направляющих косинусов:

В этом случае вычисляются три угла Эйлера, определяющие положение трех главных напряжений относительно местной системы координат (рис. 12.1):
- q (тета)- угол (нутации) между положительными направлениями осей OZ1 и N3 (0 £ q £ p);
- y (пси) - угол (прецессии) между осью OX1 и осью OA (линия пересечения плоскостей X1OY1 и N1ON2), положительное направление которой выбирается так, что OA, OZ1 и N3 образуют правую тройку. Угол y
отсчитывается от оси OX1 к OY1 (0 £ y £ 2p)
- j - (фи) - угол (чистого вращения) между осями N1 и ОA отсчитывается от оси N1 к N2 (0 £ j £ 2p).
Значения углов Эйлера определяются так:
q = arccos (n3) (12.12)
При q = 0, j = 0, y = arcsin (m1),
причем если l1
< 0, то y
= p-arcsin
(m1).
Если y < 0, то y
=y
+2p
. (12.13)
При q ¹ 0


то

Если y < 0, то y
=y
+2p
. (12.14)
Далее

причем если

то

Если j < 0, то j
= j
+2p
.
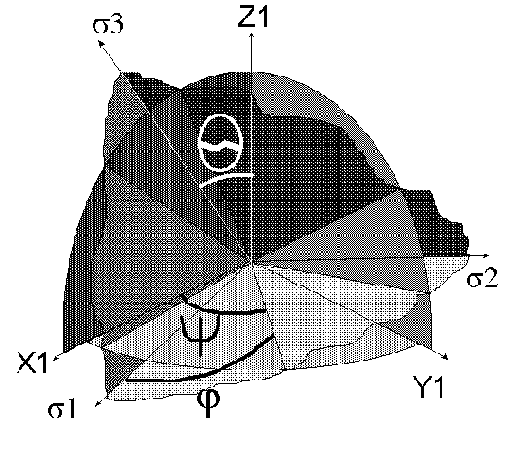
Рис. 12.1
