СУПЕРЭЛЕМЕНТНОЕ МОДЕЛИРОВАНИЕ
В ПК ЛИРА реализована возможность работы с суперэлементной расчетной моделью. На количество неизвестных не налагается никаких ограничений. Выбор разбивки схемы на суперэлементы или только на конечные элементы остается за пользователем.
Использование суперэлементов целесообразно в следующих основных случаях:
· предполагаемая размерность задачи при конечно-элементной разбивке превосходит возможности компьютера (память, быстродействие, плохая обусловленность матрицы);
· в задаче содержится большое количество идентичных конструктивных элементов (панели, объемные блоки и т.п.);
· в задаче присутствуют типовые конструктивные элементы, которые уже были сформированы для ранее рассчитанных объектов;
· в задаче имеет место локальное сосредоточение нелинейно деформируемых элементов.
Часто встречается ситуация, когда задача содержит несколько разнородных объектов, которые различаются по материалу, по набору конечных элементов, по геометрии и т.п. Это может, например, быть силосный комплекс, связанный галереями и опирающийся на плиту на упругом основании. Представление такого объекта в виде конечно-элементной схемы приводит к очень большой размерности задачи, а расчленение его на суперэлементы может существенно ее уменьшить. В этом случае расчетная модель может состоять из трех типов суперэлементов: первый - плита на упругом основании, второй - силосная башня и третий - конструкция галереи.
Еще пример. При расчете панельных домов мелкая разбивка каждой панели приводит к большой размерности задачи, а применение суперэлементов позволяет существенно снизить влияние размерности подобных задач на скорость их выполнения. При этом еще следует учесть, что количество типов суперэлементов в подобных задачах, как правило, невелико.
Существенного сокращения времени счета можно достичь при решении нелинейных задач, в которых присутствуют крупные линейно деформируемые включения.
Например, сложные здания ( панельные или каркасные дома, силосные башни, резервуары), опирающиеся на упругое основание. Для таких зданий учет нелинейной работы основания имеет существенное значение. В этом случае надземное строение необходимо объявить суперэлементом, матрица жесткости которого на каждом шаге нелинейного расчета остается неизменной.
Применение суперэлементов требует определенного навыка, поэтому рекомендуется осваивать работу с ними только после подробного ознакомления со всеми другими возможностями ПК ЛИРА.
При использовании суперэлементной модели конструкции, основная расчетная схема рачленяется на несколько расчетных схем, которые называются схемами суперэлементов. Узлы стыковки суперэлементов с основной схемой называются суперузлами (рис. 4.1).
Алгоритм решения задачи с применением метода суперэлементов (МСЭ) основывается на следующей идеологии: пусть исследуемый объект расчленен на S подсхем (суперэлементов), которые объединяются в общую основную схему при помощи N0 узлов (суперузлов).
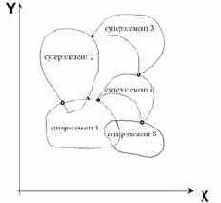
Рис. 4.1
Если через N1 обозначить количество внутренних узлов первого суперэлемента, через N2 - узлов второго и т.д., а затем пронумеровать суперузлы, то система уравнений примет вид, показанный на рис. 4.2:
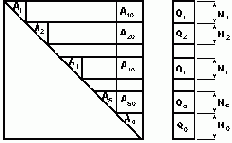
Рис.4.2
Решение задачи в такой постановке можно провести двумя способами: либо составить систему уравнений полностью и решить ее, либо составлять и решать ее по частям. Сначала составить уравнения для первого суперэлемента, т.е. А1, А10, Q1 и частично А0, Q0, затем сделать исключение N1 неизвестных. Далее проделать то же для остальных суперэлементов, сложить отдельные части А0, Q0, решить полученные уравнения, и определив перемещения суперузлов, сделать обратный ход для всей системы.
Если суперэлементы отличаются один от другого, то оба способа идентичны как в отношении количества вычислений, так и в отношении точности счета. Если же в схеме имеются одинаковые суперэлементы, то количество вычислений можно существенно сократить, если проделать все вычисления для одного из них и полученные результаты использовать для остальных суперэлементов этого же типа.
Такой подход справедлив и в том случае, когда суперэлементы одного типа различно ориентированы относительно глобальной системы координат основной схемы.
Теоретически суперэлементы в свою очередь можно расчленять на подсхемы (суперэлементы 2-го ранга), развивая этот процесс и организуя своеобразную многоранговую рекурсию. Расчленение на подсхемы обычно не вызывает особых затруднений. Как правило, оно органически связано с конструктивными особенностями объекта как, например, в зданиях из объемных блоков.
В ПК ЛИРА реализован только один ранг суперэлементов. Разработчики полагают, что в подавляющем большинстве случаев этого достаточно для описания расчетной схемы очень высокой размерности.
Рассматривая суперэлементы как конечные элементы, для которых матрица жесткости строится не аналитически, а при помощи численного расчета, можно предложить два алгоритма построения матрицы жесткости. Первый заключается в том, что на суперузлы рассматриваемого суперэлемента налагаются связи, а элементы матрицы жесткости определяются как реакции в этих связях от последовательных единичных смещений по направлению этих связей.
Другой алгоритм основывается на том, что в физическом смысле исключение j-того неизвестного по Гауссу соответствует освобождению от j-ой связи. Это приводит к следующей схеме построения матрицы жесткости: составляются канонические уравнения для всех узлов i-того суперэлемента; производится исключение N1
неизвестных, соответствующих внутренним узлам; оставшаяся часть N10 не исключенных уравнений, соответствующих суперузлам, и будет искомой матрицей жесткости
В ПК ЛИРА использован алгоритм второго типа. При этом суперузлы для суперэлемента должны нумероваться в последнюю очередь. Связанные с таким подходом затруднения в ПК ЛИРА преодолены следующим образом. Во-первых, нумерация степеней свободы для суперузлов (с учетом того, что они должны иметь последние номера) производится автоматически. Это позволяет не заботиться о порядке нумерации узлов суперэлемента. Во-вторых, в ПК ЛИРА реализован метод Гаусса, использующий существенную «разрыхленность» матрицы канонических уравнений, то есть некий симбиоз ленточного Гаусса, Гаусса с учетом «небоскребной структуры», фронтального метода, метода «спринт».
Тогда составление системы уравнений производится в компактной форме - составляется информация только о ненулевых элементах с учетом их расположения в системе уравнений, а разворачивание производится только в процессе исключения.
Информацией о наличии суперэлементов в схеме является их особая индексация в исходных данных. Каждый тип суперэлемента описывается и задается полным комплектом документов как для отдельной расчетной схемы, за исключением некоторых изменений.
После ввода исходных данных производится проверка на наличие в них суперэлементов.
При наличии суперэлементов организуется последовательный ввод исходных данных для каждого типа суперэлемента. Построение матрицы жесткости и определение супернагрузок (приведение нагрузки с области суперэлемента в суперузлы) реализованы как отдельный, специально построенный расчет.
Полученная система канонических уравнений обрабатывается неполным прямым ходом по Гауссу до неизвестных, относящихся к суперузлам. Необработанная часть системы канонических уравнений является искомой матрицей жесткости рассчитываемого суперэлемента и записывается в соответствующие наборы данных.
Аналогичным образом производится определение супернагрузок. Если нагрузка распределена по области суперэлемента, то выполняется построение столбцов правых частей канонической системы и их обработка неполным прямым ходом Гаусса. Необработанные элементы столбцов являются супернагрузками для рассматриваемого суперэлемента и записываются в соответствующие наборы данных.
После этого производится расчет основной схемы. В результате решения системы канонических уравнений основной схемы определяются перемещения суперузлов. Затем производится расчет каждого суперэлемента, который по сути является расчетом на заданные перемещения, а именно перемещения суперузлов, полученные из расчета основной схемы. Здесь используется уже имеющаяся система канонических уравнений суперэлемента, обработанная неполным прямым ходом по Гауссу. Для нее выполняются несколько (по количеству загружений) обратных ходов.И, наконец, вычисляются перемещения внутренних узлов суперэлемента и определяются остальные компоненты напряженно-деформированного состояния.
