Универсальные конечные элементы пространственной задачи теории упругости -,)

Предназначены для определения напряженно-деформированного состояния континуальных объектов и массивных пространственных конструкций из однородного изотропного линейно-упругого материала в постановке трехмерной задачи теории упругости.

Кроме того, возможно решение объемной задачи теории упругости для двухкомпонентных материалов (железобетона, композитов и т.д.), при котором один из компонентов (армирующий) обладает более высокими прочностными свойствами, чем основной (связующий). Предполагается, что армирующий материал (отдельные стержни, сетки и т.п.) расположены ортогонально осям местной системы координат элемента. Такие двухкомпонентные материалы носят название конструктивно-ортотропных.

Функционал Лагранжа при нулевых граничных условиях имеет вид:

           (1.12)

                               

где:sx(x,y,z), sy(x,y,z), sz(x,y,z), txy(x,y,z), tyz(x,y,z), tzx(x,y,z) — компоненты тензора напряжений, являющиеся непрерывными функциями координат;

 

- относительные линейные и угловые деформации;

U(x,y,z), V(x,y,z),W(x,y,z) - компоненты перемещений точек тела, параллельные соответственно осям OX,OY,OZ

общей системы координат;

Рх, Ру, Pz - компоненты интенсивности поверхностных сил, действующих в направлении осей OX, OY, OZ соответственно;

X, Y, Z -компоненты интенсивности объемных сил (на единицу объема) в направлении осей OX,OY и OZ соответственно.

Деформации и напряжения связаны между собой зависимостями:

                                               

                                                        (1.13)

                                               

                         

где:Е - модуль Юнга; n -

коэффициент Пуассона; G - модуль сдвига.

Допускается задание нагрузок на конечный элемент как в местной, так и в общей системах координат с привязкой как в местной, так и в общей системе координат, а также с привязкой в виде приращений в общей системе координат. Предусмотрены следующие виды нагрузок (табл. 1.4):

5, 15 - сосредоточенная, задаваемая относительно осей местной или общей систем координат соответственно, с привязкой в местной системе координат;

6, 16 - равномерно распределенная, задаваемая относительно осей местной и общей систем координат соответственно;

8 - температурное воздействие.

Таблица 1.4

Тип КЭ	Нагрузка	Схема и описание нагрузки	Информация, задаваемая в документах
			6."Нагрузки"		7."Величины нагрузок"
			Вид нагрузки	Haправление нагрузки	Величина нагрузки и привязка
1	2	3	4	5	6
31, 33	Сосредоточенная нагрузка, действующая по направлению осей местной или общей системы координат		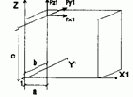5	X Y Z	Px1 (m); a, b, c (м) Py1 (m); a, b, c (м) Pz1 (m); a, b, c (м)
31, 32, 33		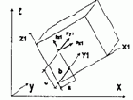	15	X Y Z	Px (m); a, b, c (м) Py (m); a, b, c (м) Pz (m); a, b, c (м)
1	2	3	4	5	6
31, 33	Равномерно распределенная нагрузка, действующая по направлению осей местной или общей систем координат (q-интенсивность нагрузки; N гр -номер грани). Если номер грани не задан или равен нулю, то нагрузка является равномерно	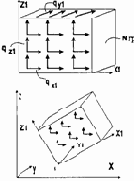N гр = 1 при Х1 = 0 N гp = 2 при Х1 = a N гр = 3 при Y1 = 0 N rp = 4 при Y1 = b N rp = 5 при Z1 = 0 N rp = 6 при Z1 = с	6 6 6	X Y Z	q ( т/м3 ), N гр
31, 32, 33, 34, 36	распределенный.по объему - собственный вес	N rp = 0	16	X Y Z	q ( т/м3 ), N гр
31, 32, 33, 34, 36	Температурное воздействие		8	0 X Y Z	t, a t, a1 t, a2 t, a3

Содержание раздела

---

---